아이템 임베딩 평균의 일관성에 대해

On the Consistency of Average Embeddings for Item Recommendation (2023)

배경

• 추천 시스템은 아이템 특성을 표현하기 위해 representation learning을 활용하는 경우가 많음
  • 즉 아이템 별로 임베딩(저차원 벡터)을 구해서 아이템 속성과 사용자의 선호도 패턴들이 이 임베딩에 반영되도록 하고, 임베딩 간의 내적이나 거리 등의 메트릭으로 유사성을 판단함
• 그렇다면 아이템의 집합은 어떻게 하나
  • 아이템의 집합이란: 여러 비디오를 가지고 있는 채널, 여러 상품을 담은 쇼핑 카트, 여러 사진을 포함하는 앨범, 여러 곡으로 구성된 재생목록, 여러 광고를 클릭한 하나의 세션
    • 심지어 유저도 그가 최근 소비한(긍정적 반응을 보인) 아이템들의 집합으로 볼 수 있음
  • 많은 경우(여러 도메인의 산업계에서) 이런 아이템의 집합(일종의 high-level concept)에 대한 representation을 얻을 때, 아이템의 임베딩을 얻을 때와 비슷한 수준의 학습 과정을 거치기보다는 집합을 이루고 있는 아이템의 임베딩을 평균 내서 사용하는 경우가 많음. 왜냐면,
    • 구현이 단순하고 범용적으로 어떤 집합에도 적용할 수 있으며 사전 계산된 아이템 임베딩만 있다면 실시간으로 바뀌는 수많은 조합에도 scalable하게 대응할 수 있음
    • 고수준 개념과의 상호작용은 개별 아이템 대비 상호작용 데이터가 희소하고 불균형할 수 있음
    • 안정적인 성능 - 구성 아이템이 충분히 유사한 경우 평균은 노이즈를 줄이고 핵심 성질을 포착할 수 있음

일관성

• 이 논문이 제기하는 문제점은 이런 상위 수준 개념(집합)에 대한 임베딩 평균을 사용하는 게 정당하냐는 것 (또는 정당성을 확인하고 사용하고 있냐는 것)
  • 아이템 임베딩을 평균내면 그 일관성이 유지되는가?
    • 평균 임베딩 $\mu U$ 가 원본 아이템의 집합 $U$ 과 유사하다 = $\mu U$ 와 유사한 아이템들이 $U$ 에 속한 아이템과 유사하다
    • ➡️ $\mu U$ 의 k개 nearest neighbors 중 실제 $U$ 에 속하는 아이템의 비율인 precision의 기대값을 측정하고 이를 일관성이라 부르겠다

$${\text{Consistency}}_k(X)={\mathbb{E}}_{U\in X_k}[{\text{Precision}}_k(U)],\text{where}{\text{Precision}}_k(U)=\frac{|X_k({\mu }_U)\cap U|}{k}$$

이론

• Proposition 1
  • 기본적으로 아이템 임베딩에 대해 각 차원이 i.i.d.이고, 유사도는 내적으로($s(x,y)=x^{T}y$) 생각함
  • 임베딩 집합 $U$ 에 대해 ${\mu }_U$ 는 해당 집합의 아이템 임베딩의 평균
  • $u_{\text{in}}$ 은 $U$ 안에 속한 아이템이고 $u_{\text{out}}$ 은 $U$ 안에 속하지 않은 아이템일 때,
    • $s_{\text{in}}=s(u_{\text{in}},{\mu }_U)$ , $s_{\text{out}}=s(u_{\text{out}},{\mu }_U)$
  • 임베딩 차원이 충분히 크고(e.g. 128차원) i.i.d 가정이 만족된다면 위의 $s$ 들(내적값)은 모두 정규분포에 근사할 수 있고, 다음과 같이 어느 한쪽이 더 클 확률을 계산할 수 있음
    • $U$ 안에 속한 아이템과 임베딩 평균의 내적이 $U$ 안에 속하지 않은 아이템과의 내적보다 클 확률이 높을수록 이 임베딩 평균의 근처에 원래 아이템들이 위치할 확률이 높다는 것이고 평균이 집합의 대표 임베딩이 되기에 적절하다는 것으로 해석할 수 있음

$$\mathbb{P}\left(s(u_{\text{in}},{\mu }_U)>s(u_{\text{out}},{\mu }_U)\right)=\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{d{\sigma }^2}{2}\sqrt{\frac{\left(2(k-1)+\kappa \right){\sigma }^2+2k\gamma \mu \sigma +2k^2{\mu }^2}{}}\right)\right]$$

• 식 안에 있는 애들은 각 차원의 왜도, 첨도, 분산, 평균 → 내적 분포를 결정하는 값들

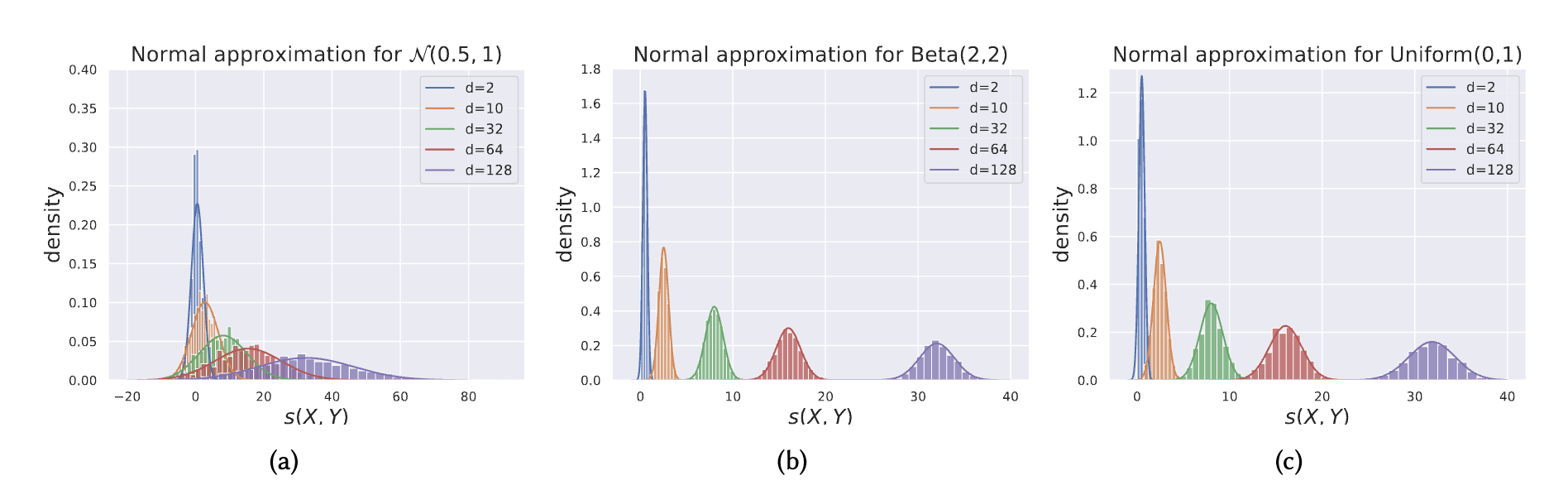
📈 벡터의 차원 수가 커질수록 내적 유사도($s$)의 분포는 정규분포에 가까워짐

• Proposition 2
  • 아이템 집합 내 임베딩 $u_{\text{in}}$ 들과 집합 외 임베딩 $u_{\text{out}}$들의 내적 유사도 분포를 통계적 순서통계량(order statistics)으로 따져서 계산
    • $f_{\text{in},(i)}(x)$ : $i$ 번째로 높은 집합 내 유사도 값에 해당하는 확률밀도함수(pdf)
      • $s_{\text{in}}$ 중 $i$번째 높은 값이 $x$ 일 확률
    • $F_{\text{out},(k-i+1)}(x)$ : $k-i+1$번째로 높은 집합 외 유사도 값에 대한 누적분포함수(cdf)
      • $s_{\text{out}}$ 중 $k-i+1$ 번째 높은 값이 $x$ 이하일 확률
    • 둘을 곱해서 적분하면 집합 내 $i$번째 similarity가 집합 밖 유사도보다는 크다는 상황에 대한 누적 확률 임
    • 이 값을 1~$k$ 까지 합치면, 평균 임베딩 주변 $k$개의 아이템 중 어느 정도가 집합 내에서 유래할 기대값 = 즉 기대 precision 값

$${\text{Consistency}}_k(X)=\frac{1}{k}\sum _{i=1}^k{\int }_{-\infty }^{\infty }{f}_{\text{in},(i)}(x)\cdot F_{\text{out},(k-i+1)}(x)dx$$

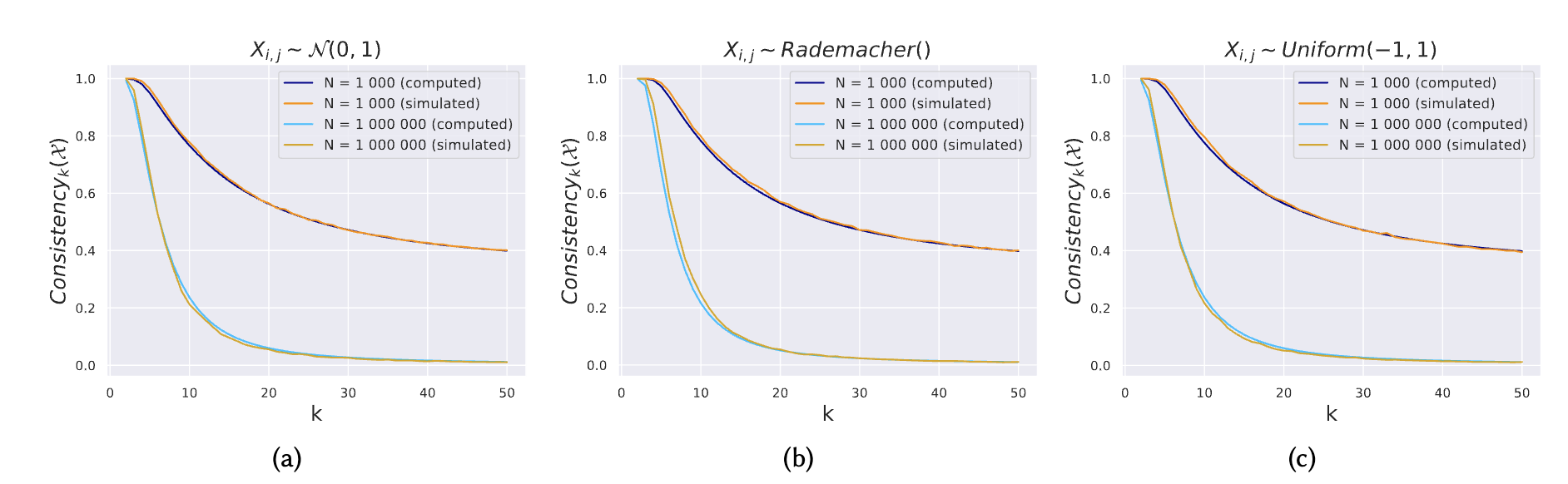
• $k$와 전체 임베딩 아이템 수 ($N$)이 커질수록 consistency는 감소함
  • $k$를 키우면 precision 떨어지는 것은 다소 당연함
  • $N$이 커져서 벡터가 많이 존재할수록 관련 없는 다른 임베딩이 우연히 평균 임베딩과 유사해질 수 있음
• $k$ 값이 작을수록 일관성 값은 $N$이 1000000 수준으로 상당히 커져도 일관성이 높게 유지됨
  • 즉 수백만 개의 아이템이 존재하는 대규모 카탈로그에서도 (이론적 가정이 지켜진다는 가정하에(?)) 작은 규모의 집합에 대해서는 평균 임베딩이 잘 대표할 수 있다 라는 결론

실험

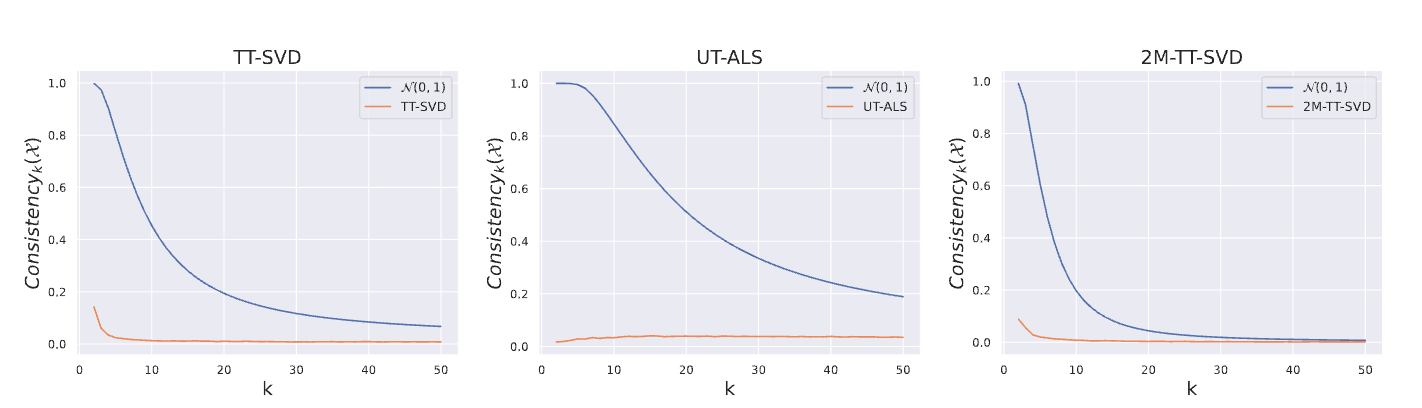
• Deezer의 음악 트랙 임베딩 데이터셋 세 가지(TT-SVD, UT-ALS, 2M-TT-SVD)를 사용하여 Consistency 값을 테스트
• 실제 데이터의 평균 임베딩은 이론적 설정의 임베딩보다 현저히 낮은 일관성을 보임
  • $k$ 값이 낮더라도(50 정도) TT-SVD는 최대 14%, 2M-TT-SVD는 6%, UT-ALS는 2% 이하의 일관성
  • SVD 기반 임베딩은 이론적 결과와 유사하게 $k$ 가 증가함에 따라 일관성 점수가 감소했지만, UT-ALS 임베딩은 약 2% 수준에서 일정한 일관성을 유지
    • UT-ALS 임베딩이 대규모 컬렉션에 대한 평균 연산에 더 적합할 수 있음을 시사
  • ❓근데 plot에서는 ALS가 20% 수준인데 본문에서는 2%라고 함. 오타라 하기엔 두번이나 2%로 나옴 ; 논지를 봤을 때도 일관성을 유지해봤자 2%면 그게 뭐가 좋은 건데요? 소리가 나오기 때문에 그냥 20%로 이해하는 게 좋을 듯
    • 사실 ALS냐 SVD냐보다도 애초에 아이템 임베딩이 어떤 방식으로 만들어진 임베딩이냐에 따라 일관성 변동이 클 수 있다 는 게 중요

추가적인 생각

• 실제로 최근에 회사에서도 (이렇게 일관성을 측정한 건 아니고 그 임베딩을 사용한 실제 retrieval 결과 지표를 봤을 때) 어떤 임베딩은 mean pooling 후에도 잘 워킹하고 어떤 임베딩은 그렇지 않은 현상을 봤기 때문에, 경험적으로도 이 결론은 맞는 결론이라 생각함
  • 임베딩 스페이스가 복잡하고 의미적으로 비선형적일수록, 희소하게 퍼져있을 수록 평균이 이상한 곳으로 가버릴 수 있을 것 같음
  • 같은 임베딩도 어떤 컬렉션으로 묶여 있냐에 따라 달라질 수 있는데 곡→ 아티스트, 영상→ 채널보다도 장바구니같은 건 상대적으로 (임베딩이 얼마나 잘 만들어졌는지와 무관하게) 일관성이 떨어질 수밖에 없을 듯
• 하지만 이런 걸 평가할 때 이런 이론 기반의 일관성 개념과 실제 downstream 추천지표 중에 뭘 보는 게 나을지가 추가적으로 궁금하긴 함(높은 일관성이 실제로 좋은 추천으로 이어지는가)
  • 일관성이 보는 건 평균 벡터가 구성원 아이템들 근처에 있어야 한다라는 좁은 의미의 대표성인데 추천의 재료로서 임베딩에 기대하는 것은 아이템 자체를 복원하는 게 아니라 그 구성원 아이템들이 암시하는 어떤 취향의 영역을 잘 포착하는 것이 아닌지