Variational Autoencoder

• VAE는 기본적으로 생성 모델(Generative Model)로, AE와는 달리 입력을 그대로 복원하는 것이 아니라 입력과 비슷하지만 새로운 데이터를 생성하는 것
  • AE: 입력 데이터를 잘 압축시킨 하나의 저차원 잠재 벡터를 얻겠다 = 특성 추출
  • VAE: 입력 데이터와 비슷하지만 다른 새로운 데이터를 얻겠다 = 생성

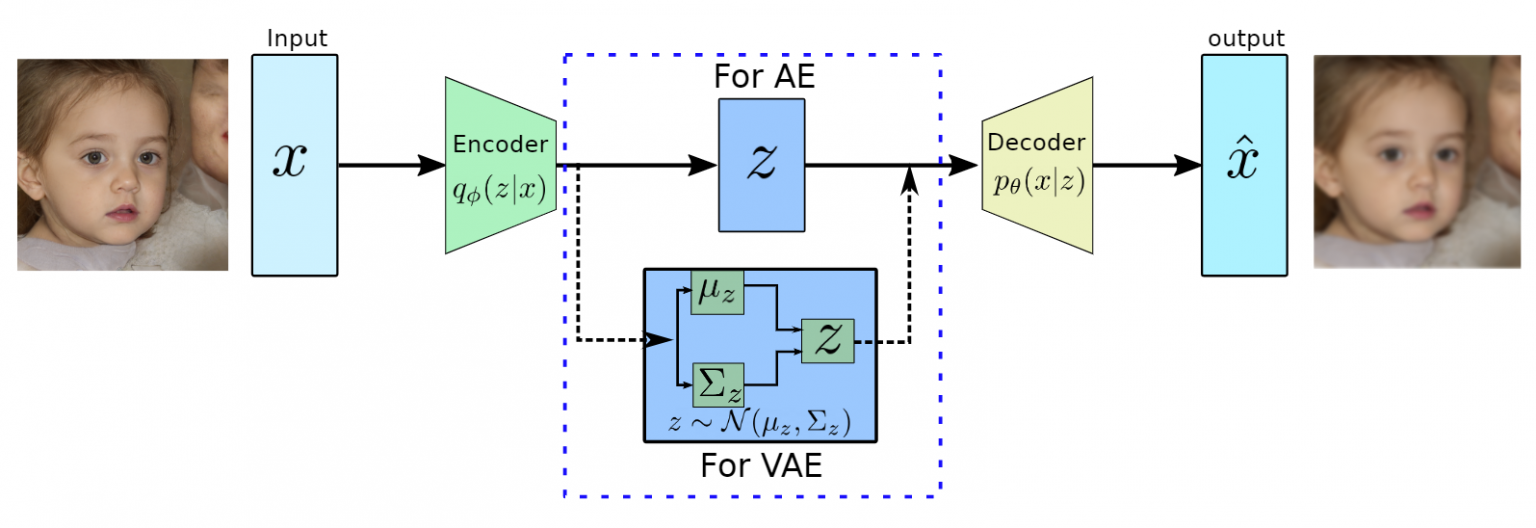
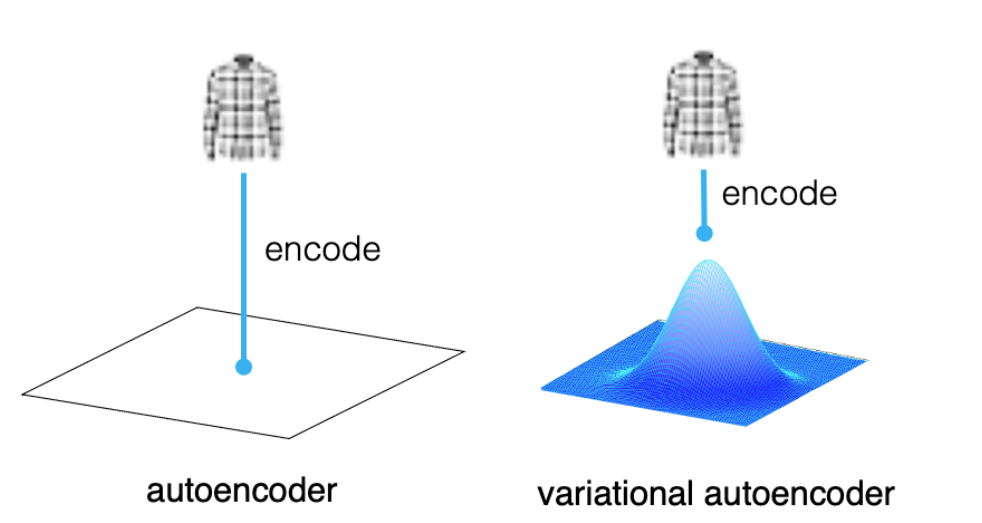
• 인코더와 디코더의 사이에 있는 병목 구간에서 잠재 벡터가 아닌 잠재 공간이 어떻게 생겼는지를 규정하는 확률 분포를 추정함

  • 즉 AE는 중간 단계에서 하나의 고정된 값을 얻는다면, VAE는 어떤 분포를 결정하는 파라미터를 얻고, 이 분포에서 샘플링을 해서 벡터를 얻고 디코더가 이 벡터를 받음
  • AE는 입력이 같으면 출력이 같을 수밖에 없는 구조이지만, VAE는 입력이 같아도 이 샘플링 때문에 다른 출력이 나올 수 있음

• 이 분포는 잘 모르니까 그냥 만만한 정규분포로 가정하자! → 변분 추론(Variational Inference)

• 인코더

  • 사실 우리가 알고 싶은 것은 잠재 공간의 진짜 사후 분포 (데이터 $x$가 주어졌을 때 $z$의 분포) - $p(z|x)$
  • 하지만 그걸 알아내는 건 너무 어려우니까 정규분포로 근사해서 랜덤 샘플링함- $q_{\Phi }(z|x)$
    • 이때 $\Phi$는 알아내야 하는 파라미터인 $\mu$, $\sigma$ 를 의미함

• 디코더

  • 샘플링한 $z$로부터 출력을 생성 - $g(x|z)$

• 아이디어는 MLE랑 유사하게 출발 - 우리의 관찰된 데이터 $x$ 가 발생할 (Log) Likelihood를 가장 높도록 하고 싶다

$$\begin{array}{rlr}\log (p(x))& =\int \log (p(x))q_{\Phi }(z|x)dz& \because \int q_{\Phi }(z|x)dz=1\\ & =\int \log (\frac{p(x,z)}{p(z|x)})q_{\Phi }(z|x)dz& \because p(x)=\frac{p(x,z)}{p(z|x)}\\ & =\int \log (\frac{p(x,z)}{q_{\Phi }(z|x)}\cdot \frac{q_{\Phi }(z|x)}{p(z|x)})q_{\Phi }(z|x)dz& \\ & =\int \log (\frac{p(x,z)}{q_{\Phi }(z|x)})q_{\Phi }(z|x)dz+\int \log (\frac{q_{\Phi }(z|x)}{p(z|x)})q_{\Phi }(z|x)dz& \end{array}$$

• 첫번째 term : $\int \log (\frac{p(x,z)}{q_{\Phi }(z|x)})q_{\Phi }(z|x)dz$ = Evidence Lower Bound
• 두번째 term : $\int \log (\frac{q_{\Phi }(z|x)}{p(z|x)})q_{\Phi }(z|x)dz$ = KL Divergence
  • $p(z|x)$ 와 $q_{\Phi }(z|x)$의 차이
    • 문제는 우리가 진짜 $p(z|x)$ 를 전혀 모르고, 주어진 고정된 데이터셋만 가지고 있다는 것
    • 따라서 이 term은 최적화가 가능한 영역이 아님
• 결국 $\log (p(x))$ = ELBO + KLD 를 최대화하는 것은 ELBO를 최대화하는 문제가 됨
  • ELBO term은 우리가 가진 데이터(증거)의 likelihood의 하한선이 되므로, 이를 Evidence Lower Bound라고 부름

\begin{align} \int \log ( \frac{p(x,z)}{q_{\Phi}(z \vert x)}) q_{\Phi}(z \vert x) dz & = \int \log ( \frac{p(x \vert z) p(z)}{q_{\Phi}(z \vert x)}) q_{\Phi}(z \vert x) dz \\ & = \int q_{\Phi}(z \vert x) \log(p(x \vert z)) dz - \int q_{\Phi}(z \vert x) \log( \frac{q_{\Phi}(z \vert x)}{p( z)}) dz \\ & = E_{q_{\Phi}} \log(p(x \vert z)) - KL(q_{\Phi}(z \vert x ) \Vert p(z)) \end{align}

• 첫번째 term : $E_{q_{\Phi }}\log (p(x|z))$
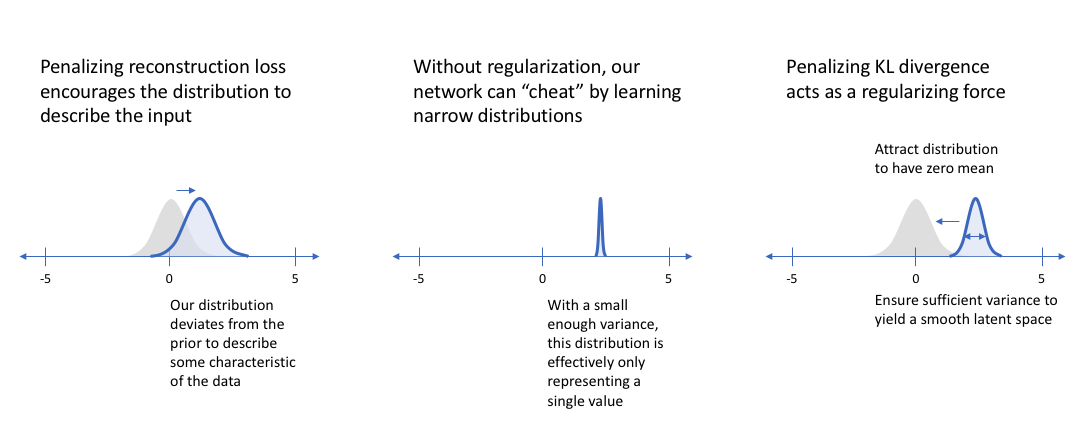
  • $q$를 써서 $x$에서 $z$를 얻고, $z$로부터 생성된 $x$를 얻는데 이게 원래 입력인 $x$와 최대한 비슷하도록 (negative 크로스엔트로피임)
  • 즉 오토인코더의 Reconstruction Loss 가 최대한 적도록!
• 두번째 term: $KL(q_{\Phi }(z|x)\Vert p(z))$
  • 실제 $z$의 분포와 우리가 가정한 정규분포가 최대한 비슷하도록! (위에 한번 등장한 KLD와는 대상이 다른 점 주의)
  • 두 개의 분포 차이가 작아지도록 하여 Regularization으로 작용

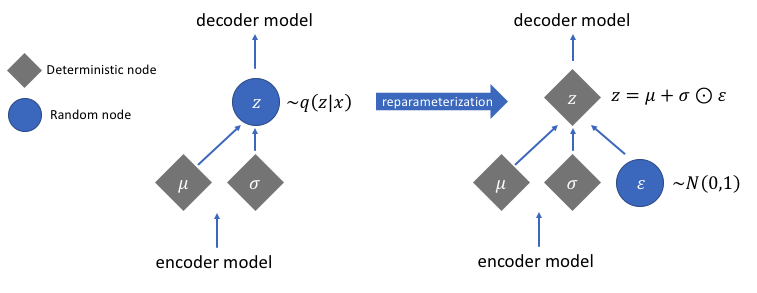
• 재파라미터화 테크닉
  • VAE는 중간에 확률분포로부터 랜덤샘플링을 하는데, 문제는 랜덤샘플링은 backpropagation이 안 됨!
  • 샘플링한 벡터를 다음과 같이 표현해서 해결

$z=\mu +\sigma \cdot ϵ$

• 여기서 $ϵ$은 표준정규분포(평균이 0, 분산이 1인 정규분포)에서 샘플링한 노이즈 변수
• 이렇게 하는 것이나 처음부터 평균이 $\mu$이고 분산이 ${\sigma }^2$인 분포에서 샘플링을 하는 것이나 사실 같은 소리이지만, 랜덤성이 존재해서 기울기 계산이 안 되는 부분을 모델 학습과 무관한 고정된 분포를 따르는 $ϵ$에 제한함으로써 역전파가 가능하게 됨

참고

• 오토인코더의 모든 것 - 강의, 슬라이드
• VAE 논문
• VAE 설명 (Variational autoencoder란? VAE ELBO 증명)
• 변분추론(Variational Inference)